启华高中的数学“拆招法”：四步唤醒你的解题潜能

面对复杂的数学式子，许多同学的第一反应是“被吓住”。欧阳晔老师却告诉我们：数学的可怕之处，往往在于“想象力的封印”。

比如例1中看似吓人的最小值问题，用基本不等式或数形结合都能破解。关键在于，你是否愿意主动拆解题目，尝试不同路径？

就像拆解一团乱麻，找到线头（已知条件），再顺着逻辑（公式、图形）一点点梳理。数学思维的第一步，是学会把“难题”转化为“可操作的步骤”，而非被表象吓退。  

例2的蚂蚁爬行问题，生动地展示了数学的“变形术”。

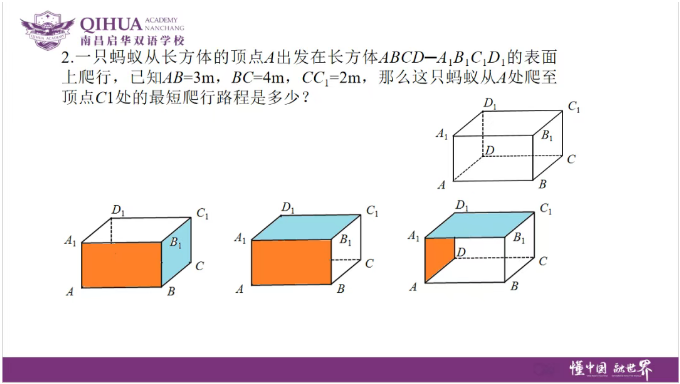
立体几何中，最短路径看似复杂，但只需将空间展开成平面，问题便迎刃而解。

欧阳晔老师强调的“转化思维”，正是数学的灵魂：将陌生问题转化为熟悉模型，将抽象条件具象化。

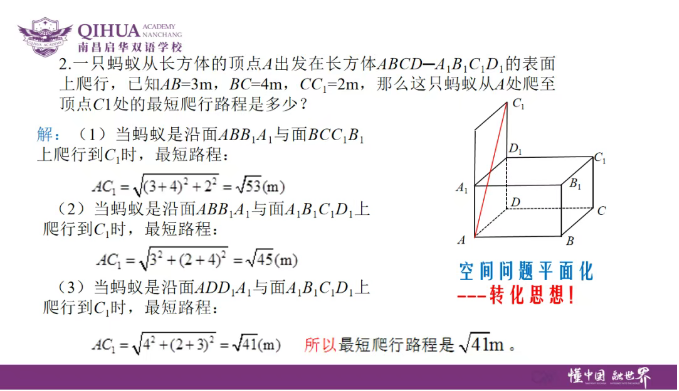
这种能力不仅适用于数学，语文学习中同样需要——比如将晦涩的古文转化为现代故事，将作文主题转化为生活场景。学会“转化”，就是学会用已知的工具解决未知的问题。

欧阳晔老师提出的“每天20分钟高强度训练”，绝非题海战术，而是针对思维短板的精准锻炼。

就像运动员反复打磨一个动作，数学思维也需要在“做—思—究”的循环中强化：做题时聚焦卡点，复盘时追问“为什么没想到”，探究时尝试一题多解。

这种训练不是机械重复，而是让大脑适应“主动出击”的状态。真正的提升，源于对过程的深度参与。  

许多学生忽略的“整理”环节，恰恰是欧阳晔老师最重视的“思维结晶”。

错题本不是罚抄本，而是记录“当时为什么错”和“下次如何对”的思维地图；灵感笔记则捕捉解题中的“灵光一现”，比如例1中数形结合的灵感可能源于某次课堂联想。

整理，是让零散的思考生根发芽的过程。

欧阳晔老师的四步法，不仅是解题秘诀，更是一种学习哲学。

当你开始用思维的眼睛看世界，所有的知识都会向你敞开大门。